Universidad Central del Este UCE Descripción General: El presente análisis introduce el concepto de dos nuevos tipos de funciones:
|
Objetivo(s) General(es): -Dotar al estudiante del lenguaje e instrumental matemático indispensables para la formulación de los problemas de las ciencias y tecnologías propias de la ingeniería. -Valorar la importancia del cálculo como instrumento para la modelación y solución de problemas reales y lograr, de este modo, establecer un vínculo entre la matemática y la realidad. Sistema de Evaluación: 30 % Calificación Acumulada: Hasta la 6ta Semana 30 % Calificación Acumulada: Desde la 7ma hasta 11va Semana 40 % Calificación: 15ta - 16ta Semana (Evaluación Final) Bibliografía Básica Edwin J. Purcell y Dale Varberg, Calculo con geometría Analítica. Editora Prentice Hall. Larson Hostetler Ewards, Calculo y geometría Analítica. 6ta Edición. Editora. MC Graw Hill. George F. Simimons, Calculo y geometría Analítica. 6ta Edición. Editora. MC Graw Hill. Bibliografía Complementaria Marcelino Grullon, trabajo de Investigación sobre los Orígenes del Calculo y sus Aplicaciones. TEMA 1 Series Infinitas 1-1 Sucesiones infinitas En un lenguaje sencillo, una sucesión  es un arreglo ordenado de números reales, uno para cada entero positivo. Más formalmente, una sucesión infinita es una función cuyo dominio es el conjunto de enteros positivos y cuyo rango es un conjunto de números reales. Dominio El dominio de una función es el conjunto de existencia de la misma, o sea los valores para los cuales la función está definida. Podemos indicar una sucesión mediante  o simplemente por  Dar click en : http://ed21.webcindario.com/id372.htm para ver mas. En algunos casos,extenderemos un poco este concepto permitiendo que el dominio conste de todos los enteros mayores o iguales a un entero específico, como en  que denotamos como  Se puede especificar una sucesión dando suficientes términos iniciales para establecer un patrón, como en 1,4,7,10,13, ... mediante una fórmula explícita para el n-ésimo término, como en  o mediante una fórmula recursiva  Observe que cada una de estas ilustraciones describe la misma sucesión. He aquí otras cuatro fórmulas explícitas y los primeros términos de las sucesiones que generan  Convergencia Considere las cuatro sucesiones recién definidas. Cada una tiene valores que se apilan cerca de 1. Pero, ¿todas convergen a {an} y {bn}convergen a l, pero {cn} y {d n} no Para que una sucesión converja a 1, primero debe ocurrir que los valores de la sucesión se acerquen a 1. Pero deben hacer algo más que estar cerca; deben permanecer cerca, para toda n más allá de cierto valor. Esto descarta a la sucesión {cn}. Además, cerca significa arbitrariamente cerca, es decir, dentro de cualquier distancia no nula dada con respecto de 1, lo cual excluye a {d n}. Aunque la sucesión {dn} no converge a l, es correcto decir que converge a 0.999. La sucesión cn} no converge; decimos que diverge Teoremas de límites Teorema principal de los límites Teorema A Sean n un entero positivo, k una constante y f y g funciones que tengan límites en c. Entonces.  Aplicaciones del teorema principal de los límites En los ejemplos siguientes, los números dentro de un círculo se refieren al número de la afirmación del teorema A. Cada igualdad está justificada por la afirmación indicada.   1-2 Series infinitas Definición La sucesión {an} se dice que converge a L y escribimos 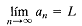 si para cada número positivo ε existe un número positivo correspondiente a N tal que  Si no hay un número finito L al que converja una sucesión, se dice que ésta diverge, o que es divergente. EJEMPLO 1 Demuestre que si p es un entero positivo, entonces  SOILUCIÓN Sea ε > 0 arbitrario dado. Elegimos N como cualquier número mayor que  Entonces  implica que    Teorema del emparedadoSuponga que {an} y {cn} convergen a L y que  (K es un enterofijo). Entonces {bn} también converge en L. P R A C T I C A No 1: Conjunto de problelnas 9.1 En los problemas del 1 a l0 se da una fórmula explícita para an Escriba los primeros cinco términos de {an}, determine si la sucesión converge o diverge y, si converge, determine    En los problemas del 31 al36 escriba los primeros cuatro términos de la sucesión {an }.  Serie geométrica Una serie de la forma  donde  es una serie geométrica     Series positivas: el criterio de la integral Siempre hay dos preguntas importantes sobre una serie. 1. ¿La serie converge? 2. Si converge, ¿cuál es su suma? ¿Cómo contestar a estas preguntas? Alguien podría sugerir el uso de una computadora. Para responder la primera pregunta, basta sumar más y más términos de la serie, observando los números obtenidos como sumas parciales. Si estos números parecen estabilizarse en un número fijo S, la serie converge. Y en este caso, S es la suma de la serie, lo cual responde a la segunda pregunta. Esta respuesta simplemente es incorrecta para la primera pregunta y sólo es parcialmente adecuada para la segunda. Veamos por qué. Considere la serie armónica  Sabemos que esta serie diverge, pero una computadora no nos ayudaría a descubrir este hecho. Las sumas parciales Sn de esta serie crecen sin límite, pero lo hacen tan lentamente que se necesitan más de 272 millones de términos para que Sn alcance 20 y más de 1043 términos para que Sn llegue a 100. Debido a la limitación inherente en el número de dígitos que puede manejar, una computadora daria en algún momento valores repetidos para Sn lo cual sugeriría incorrectamente que las Sn estarían convergiendo. Lo que es cierto para la serie armónica es cierto para cualquier serie que diverge lentamente. Enfatizamos lo siguiente: una computadora no puede sustituir los criterios matemáticos para la convergencia y la divergencia, tema que tratamos a continuación. . En ésta y la próxima sección restringimos nuestra atención a las series con términos positivos (o al menos no negativos). Con esta restricción podremos dar algunos criterios de convergencia notablemente sencillos. Sumas parciales acotadas. Nuestro primer resultado es consecuencia directa del teorema de la sucesión monótona. Teorema A: Criterio de la suma acotada Una serie  de términos no negativos converge si y sólo si sus sumas parciales están acotadas por arriba  Observemos que el entero 1 puede reemplazarse por cualquier entero positivo en este teorema.   Series de potencias Hasta ahora hemos estudiado lo que podría llamarse series de constantes,es decir, series de la forma  :,donde cada un es un número. Ahora estudiaremos las series de funciones, series de la forma ":,un(x). Un ejemplo típico de esta clase de series es  Por supuesto, en cuanto sustituimos un valor de x (como x = 2.1), regresamos a territorio familiar; tenemos una serie de constantes. Hay dos preguntas importantes en cuanto a una serie de funciones. 1. ¿Para qué valores de x converge la serie? 2. ¿A qué función converge? Es decir, ¿cuál es la suma S(x) de la serie? |
Sin embargo, incluso en el cálculo elemental podemos aprender mucho en el caso particular
de una serie de potencias.
Una serie de potencias en x tiene la forma
(Aquí interpretamos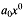 
como ao incluso cuando x = 0). Podemos responder de inme-
diato nuestras dos preguntas en el caso de una serie de potencias.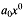como ao incluso cuando x = 0). Podemos responder de inme-
En los problemas del 31 al 36 escriba los primeros cuatro términos dela sucesión {an}
TEMA 2
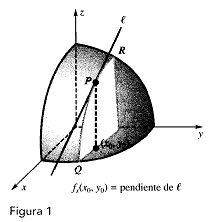
Derivadas ParcialesSuponga que f es una función de dos variables x e y. Si y se mantiene constante, digamos, y = yo, entonces
f(x, yo) es una función de la variable simple x. Su derivada en x = xo es la derivada parcial defrespecto a x en (xo, yo) y se denota fx (xo, yo). Así,
De manera análoga, la derivada parcial de f respecto a y en (xo, yo) se denota fy (xo, yo)
y está dada por
En vez de calcular fx ((xo yo) y, fy(xo, yo) directamente a partir de las definiciones en los recuadros, por lo general hallamos fx(x, y) y fy(x, y) usando las reglas usuales para las derivadas; luego, sustituimos x = xo y, y = yo.
Aquí, el punto importante es que las regIas para la derivación de una función de una variable sirven para determinar las derivadas parciales, siempre que se mantenga fija una variable.
Derivadas parciales de orden superior
Como una derivada parcial de una función de x e y , es, en general, otra función de estas mismas dos variables, se puede derivar parcialmente respecto a x o y, con lo que se obtienen las segundas derivadas
parciales de f,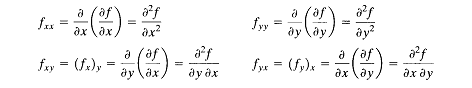
E J E M P L O:
Encuentre las cuatros segundas derivadas parciales de f(x , y ) = x ey - sen ( x/y) + x3 y2
Solución:1.- Observar que la primera derivación es un producto x ey y la segunda es
d (sen v) = cos v dv / dx en la que v = x / y
dx
2.- Observar que ey se deriva con la tabla, donde buscamos
dev= evdv/dx
dx
3.- Es necesario tener presente que cuando derivamos con respecto a una variable la otra permanece como una constante.
1ERA Derivada de Z con respecto a x.Si Z = f(x , y)
∂Z = ∂{x(∂ ey) + ∂( x ).(ey)}- ∂(sen x /y) + ∂(x3 y2)
∂x (∂x) ∂x ∂x ∂x
∂Z = {x.0 +1.ey}-cos (x/y) ∂(x/y) +3 x2 y2
∂x ∂x
∂Z =ey-cos (x/y)(1.y – x . 0)+3x2 y2
∂x y2
∂Z = ey-1 / y.cos ( x/y ) +3x2 y2
∂x
1ERA Derivada de Z con respecto a y.Si Z = f(x ,y)
∂Z = { x (∂ ey) + ∂( x ). (ey) } - ∂( sen x /y ) + ∂( x3 y2 )
∂y (∂y) ∂y ∂y ∂y
d Z = { x.ey + 0 . ey } - cos ( x/y ) ∂(x/y) + 2x3 y
d Z = { x.ey + 0 . ey } - cos ( x/y ) ∂(x/y) + 2x3 y
d y ∂y
∂Z = x . ey - cos ( x/y ) (0 .y – 1 . x ) + 2 x3 y
∂y y2
∂Z = x . ey - cos ( x/y ) ( - x ) + 2x3 y
∂y y2
∂Z = x ey + ( x ) cos ( x/y ) + 2x3 y
∂y y2
2DA Derivada Parcial de Z con respecto a x. Conocemos el resultado de la primera derivada de Z con respecto a x , para hallar la segunda derivada de Z con respecto a x, solo debemos derivar nuevamente.∂Z = ey - 1 / y . cos ( x/y ) + 3x2 y2
∂x
∂2 Z = ∂ey + ∂{-1 / y . cos ( x/y ) } + ∂(3x2 y2 )
∂x2 ∂x ∂x ∂x
∂x2 ∂x ∂x ∂x
∂2Z = 0 + { ∂ ( -1 / y) }. cos ( x/y ) + {∂cos ( x/y ) } (-1 / y) + ∂( 3x2 y2 )
∂x2 ∂x ∂x ∂x
∂2 Z = { 0 . y – 1 . 0 } cos ( x/y ) - sen( x/y ) d ( x/y ) (-1 / y) } + 6 x y 2
∂x2 y2 d x
∂2 Z = - sen( x/y ) (1 . y – 0 . 1) (-1 / y) } + 6 x y 2
∂x2 y2
∂2 Z = - sen( x / y ) (1 ) (-1 / y) + 6 x y 2
∂x2 y
∂2Z = - 1 / y2. - sen( x/y ) + 6 x y 2
∂x2
∂2Z = 1 / y2. sen ( x/y ) + 6 x y 2
∂x2
2DA Derivada Parcial de Z con respecto a y.
2DA Derivada Parcial de Z con respecto a y. Conocemos el resultado de la primera derivada de Z con respecto a y, para hallar la segunda derivada de Z con respecto a y, solo debemos derivar nuevamente. ∂Z = x ey + x cos ( x / y ) + 2x3 y
∂y y2
∂2 Z = ∂(xey) + ∂{( x ) . cos ( x/y )} + ∂ (2x3 y)
∂y2 ∂y ∂y (y2) ∂y
∂2 Z ={∂ (x )} . ( ey) + ∂ {( ey)} . (x ) }+ {∂ ( x )}.cos ( x/y ) +∂{cos ( x/y )} .( x ) ]2x3
∂y2 ∂y ∂y ∂y ( y2) ∂y ( y2)
∂y2 ∂y ∂y ∂y ( y2) ∂y ( y2)
∂2Z = { (0 ) . ( ey) + ey . (x ) } + { 0 . (y2) – 2y (x) } cos ( x/y ) -
∂y2 ( y 4)
- {sen ( x/y ) . d( x/y ) } . ( x2 ) + 2 x3
d y ( y )
∂2 Z = ey . x + [– 2y (x) ]. cos ( x/y ) - [ sen ( x/y ) ( 0. y - 1. x ) ] . x / y 2 + 2 x3
∂y2 (y4) y 2
Simplificando y reordenando.∂2 Z = x ey - x2 / y 4 sen ( x/y ) – 2 x / y 3 cos ( x/y ) + 2 x3
∂ y2
Derivada Parcial de f con respecto a y de Parcial de f con respecto a x.fxy = (fx)y = ∂ (∂ f ) = ∂2f
∂y (∂x) ∂y∂x
Sabemos de la derivación anterior.∂Z = ey - 1 / y .cos ( x/y )+ 3x2 y2
∂x
∂ (∂Z ) = ∂2 Z = ∂ey – ∂[1 / y .cos ( x/y ) ] + ∂ (3x2 y2)
∂y (∂x) ∂y∂x ∂y ∂y ∂y
Tarea. 1.- Concluir este ejercicio. 2.- encontrar la siguiente derivada. fyx = ( fy )x = ∂ (∂ f ) = ∂2 f
∂x (∂y) ∂x∂y
PRACTICA No3
(Capitulo 12, pag.628 Purcell 9na.Edic.)
PRACTICA No3
(Capitulo 12, pag.628 Purcell 9na.Edic.)
La regla de la cadena
Si y = f(x(t», donde fy x son funciones diferenciables, entonces
Primera versión
Si z = f(x, y), donde x y y son funciones de t, entonces tiene sentido preguntarse por dz/dt, y por lo tanto debe existir una fórmula para ella.
Segunda versión
Suponga que z =f(x, y), donde x = x(s, t) y y(s, t). Entonces tiene sentido preguntarse por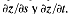
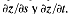
Tema 3
Integrales múltiples
Aplicar el concepto de integración para calcular volúmenes de cuerpos en el espacio
Integrales dobles sobre rectángulos
La cuestión de la existencia
No toda función de dos variables es integrable en un rectángulo dado R. Las razones son las mismas que en el caso de una variable.
En particular, una función que no esté acotada en R no es integrable.
Teorema A : Teorema de integrabilidad
Si f está acotada en el rectángulo cerrado R y si es continua allí, excepto en un número finito de curvas suaves, entonces f es integrable en R.
En particular, si f es continua en todo R, entonces f es integrable.
La función escalonada de la figura 5 es integrable en R porque sus discontinuidades ocurren a lo largo de dos segmentos de recta.
Propiedades de la integral doble
La integral doble hereda la mayoría de las propiedades de la integral sencilla.
1. La integral doble es lineal; es decir,
2. La integral doble es aditiva en rectángulos (figura 6) que se traslapan sólo en un segmento de recta.
3. Se cumple la propiedad de comparación. Si f(x, y) ~ g (x, y) para todo (x, y) en R, entonces
Evaluación de integrales dobles
Observe primero que si f(x, y) = 1 en R, entonces la integral doble es el área de R, y de esto se sigue que
EJEMPLO 1 Sea fla función escalonada de la figura 5;
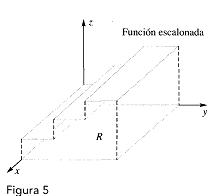
es decir, sea:
