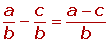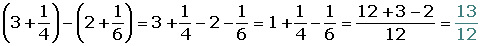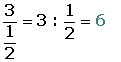Repaso de operaciones con fracciones

Suma y resta de fracciones 

Con el mismo denominador.

Se suman o se restan los numeradores y  se mantiene el mismo denominador.

Con distinto denominador

1. Se reducen los denominadores a común denominador:

1º Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.

2º Este denominador, común, se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.

2. Se suman o se restan los numeradores de las fracciones equivalentes obtenidas.

Multiplicacion de fracciones

El producto de dos fracciones es otra fracción que tiene:

• Por numerador el producto de los numeradores.
• Por denominador el producto de los denominadores.

División de fracciones

El cociente de dos fracciones es otra fracción que tiene:

• Por numerador el producto de los extremos.
• Por denominador el producto de los medios.

Ejercicio de operaciones con fracciones

Una caja contiene 60 bombones. Eva se comió 1/5 de los bombones y Ana 1/2.

1 ¿Cuántos bombones se comieron Eva, y Ana?
2¿Qué fracción de bombones se comieron entre las dos
Un padre reparte entre sus hijos 1800 €. Al mayor le da 4/9 de esa cantidad, al mediano 1/3 y al menor el resto. ¿Qué cantidad recibió cada uno? ¿Qué fracción del dinero recibió el tercer

Ejercicio de operaciones con fracciones
Una familia ha consumido en un día de verano:

• Dos botellas de litro y medio de agua.
• 4 botes de 1/3 de litro de zumo.
• 5 limonadas de 1/4 de litro.

¿Cuántos litros de líquido han bebido? Expresa el resultado con un número mixto.

Calcula las siguientes operaciones con fracciones:

 

  1.-

2.-

3.-

4.-

Efectúa las divisiones de fracciones:

1.-   

     

2.-

 

3.-

Potencias de fracciones

Para elevar una fracción a una potencia se eleva tanto el numerador como el denominador al exponente.

 

Potencias de exponente negativo

 

 

 

 

 

Propiedades de las potencias de fracciones

1.-  

 

2.-

3. Producto de potencia con la misma base

 Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.

4. División de potencias con la misma base:

Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.

5. Potencia de una potencia

Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes.

6. Producto de potencias con el mismo exponente:
Es otra potencia con el mismo exponente y cuya base es el producto de las bases

7. Cociente de potencias con el mismo exponente:
Es otra potencia con el mismo exponente y cuya base es el cociente de las bases.

 

 

Ejercicios de potencias de fracciones

Realiza las siguientes operaciones con potencias de fracciones:

1. 

2.  

3.  

4.

5.  

6. 

7. 

8.  

9. 

10

11.   

12.  

13

Operaciones combinadas de fracciones

Prioridades

1º.Pasar a fracción los números mixtos y decimales.

2º.Calcular las potencias y raíces

3º.Efectuar las operaciones entre paréntesis, corchetes y llaves..

4º.Efectuar los productos y cocientes.

5º.Realizar las sumas y restas.

Ejercicios de operaciones combinadas con fracciones

Primero operamos con las productos y números mixtos de los paréntesis.

Operamos en el primer paréntesis, quitamos el segundo, simplificamos en el tercero y operamos en el último.

Realizamos el producto y lo simplificamos.

Realizamos las operaciones del paréntesis.

Hacemos las operaciones del numerador, dividimos y simplificamos el resultado.

Opera:

Comparación de fracciones

Fracciones con igual denominador

De dos fracciones que tienen el mismo denominador es menor la que tiene menor numerador.

Fracciones con igual numerador

De dos fracciones que tienen el mismo numerador es menor el que tiene mayor denominador.

Con numeradores y denominadores distintos

En primer lugar las tenemos que poner a común denominador.

Es menor la que tiene menor numerador.

Ejercicios de comparar fracciones

Escribe el signo > o <, donde corresponda.

Compara las siguientes fracciones:

Ordenar de menor o mayor las siguientes fracciones::

Dos automóviles A y B hacen un mismo trayecto de 572 km. El automóvil A lleva recorrido los 5/11 del trayecto cuando el B ha recorrido los 8/13 del mismo. ¿Cuál de los dos va primero? ¿Cuántos kilómetros llevan recorridos cada uno?

El segundo automóvil va primero.

Los 2/5 de los ingresos de una comunidad de vecinos se emplean combustible, 1/8 se emplea en electricidad, 1/12 en la recogida de basuras, 1/4 en mantenimiento del edificio y el resto se emplea en limpieza.

¿Qué fracción de los ingresos se emplea en limpieza?

De acuerdo con la fracción de ingresos empleada, ordena las partidas enumeradas de menor a mayor

Fracción generatriz

Un número decimal exacto o periódico puede expresarse en forma de fracción, llamada fracción generatriz, de las formas que indicamos:

Pasar de decimal exacto a fracción

Si la fracción es decimal exacta, la fracción tiene como numerador el número dado sin la coma, y por denominador, la unidad seguida de tantos ceros como cifras decimales tenga.

Pasar de periódico puro a fracción generatriz

Si la fracción es periódica pura, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera, y por denominador un número formado por tantos nueves como cifras tiene el período.

Pasar de periódico mixto a fracción generatriz

Si la fracción es periódica mixta, la fracción generatriz tiene como numerador el número dado sin la coma, menos la parte entera seguida de las cifras decimales no periódicas, y por denominador, un numero formado por tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga la parte decimal no periódica.

Ejercicios de fracción generatriz

Pasar a fracción generatriz:

Pasar a fracción generatriz:

Realizar las siguientes operaciones:

1

2

3